El aprendizaje multitarea en redes neuronales profundas

A Spanish translation reviewed & postedited by Chema, a Spain-based translation student specializing in English to Spanish translations

An original text written by Sebastian Ruder, originally published in
https://www.ruder.io/multi-task/

El aprendizaje multitarea es cada vez mas popular. Esta publicación ofrece una descripción general del estado actual del aprendizaje multitarea. En particular, proporciona contexto para los métodos actuales basados ​​en redes neuronales al analizar la extensa literatura de aprendizaje multitarea.

Esta publicación ofrece una descripción general del estado actual del aprendizaje multitarea.

Nota: Este artículo está también disponible en arXiv.

INDICE

• Introducción
• Motivación
• Dos métodos MTL para Deep Learning
  • Compartir parámetros duros
  • Compartir parámetros suaves
• ¿Por qué funciona MTL?
  • Aumento de datos implícito
  • centrando la atencion
  • escuchar a escondidas
  • Sesgo de representación
  • regularización
• MTL en modelos no neuronales
  • Regularización de bloques escasos
  • Relaciones de tareas de aprendizaje
• Trabajo reciente sobre MTL para aprendizaje profundo
  • Redes de relaciones profundas
  • Uso compartido de funciones totalmente adaptable
  • Punto de Cruz Redes
  • Baja supervisión
  • Un modelo conjunto de muchas tareas
  • Ponderación de pérdidas con incertidumbre
  • Tensorización factorial para MTL
  • Redes de Esclusas
  • ¿Qué debo compartir en mi modelo?
• Tareas auxiliares
  • Tarea relacionada
  • Adversario
  • Sugerencias
  • Centrando la atención
  • Suavizado de cuantización
  • Entradas de predicción
  • Usar el futuro para predecir el presente
  • Aprendizaje de representación
  • ¿Qué tareas auxiliares son útiles?
• Conclusión

Introducción

En Machine Learning (ML), normalmente nos preocupamos por optimizar para una métrica en particular, ya sea una puntuación en un punto de referencia determinado o un KPI comercial. Para hacer esto, generalmente entrenamos un solo modelo o un conjunto de modelos para realizar la tarea deseada. Luego ajustamos y ajustamos estos modelos hasta que su rendimiento ya no aumenta. Si bien generalmente podemos lograr un rendimiento aceptable de esta manera, al concentrarnos en nuestra única tarea, ignoramos la información que podría ayudarnos a mejorar aún más la métrica que nos interesa. Específicamente, esta información proviene de las señales de entrenamiento de tareas relacionadas. Al compartir representaciones entre tareas relacionadas, podemos permitir que nuestro modelo generalice mejor nuestra tarea original. Este enfoque se llama aprendizaje multitarea (MTL) y será el tema de esta publicación de blog.

El aprendizaje multitarea se ha utilizado con éxito en todas las aplicaciones de aprendizaje automático, desde el procesamiento del lenguaje natural ^[1] y el reconocimiento de voz ^[2] hasta la visión artificial ^[3] y el descubrimiento de fármacos ^[4] . MTL se presenta de muchas formas: aprendizaje conjunto, aprender a aprender y aprender con tareas auxiliares son solo algunos nombres que se han utilizado para referirse a él. En general, tan pronto como se encuentra optimizando más de una función de pérdida, está realizando efectivamente un aprendizaje de tareas múltiples (en contraste con el aprendizaje de una sola tarea). En esos escenarios, ayuda pensar en lo que está tratando de hacer explícitamente en términos de MTL y extraer ideas de ello.

Incluso si solo está optimizando una pérdida como es el caso típico, es probable que haya una tarea auxiliar que lo ayude a mejorar su tarea principal. Rich Caruana ^[5] resume el objetivo de MTL de manera sucinta: “MTL mejora la generalización al aprovechar la información específica del dominio contenida en las señales de entrenamiento de tareas relacionadas”.

En el transcurso de esta publicación de blog, intentaré brindar una descripción general del estado actual del aprendizaje multitarea, en particular cuando se trata de MTL con redes neuronales profundas. Primero motivaré a MTL desde diferentes perspectivas. Luego, presentaré los dos métodos empleados con más frecuencia para MTL en Deep Learning. Posteriormente, describiré los mecanismos que juntos ilustran por qué MTL funciona en la práctica. Antes de ver métodos MTL basados ​​en redes neuronales más avanzados, proporcionaré algo de contexto al analizar la literatura en MTL. Luego, presentaré algunos métodos propuestos recientemente más potentes para MTL en redes neuronales profundas. Finalmente, hablaré sobre los tipos de tareas auxiliares de uso común y discutiré qué hace que una buena tarea auxiliar para MTL.

Motivación

Podemos motivar el aprendizaje multitarea de diferentes maneras: Biológicamente, podemos ver el aprendizaje multitarea como inspirado por el aprendizaje humano. Para aprender nuevas tareas, a menudo aplicamos el conocimiento que hemos adquirido al aprender tareas relacionadas. Por ejemplo, un bebé primero aprende a reconocer rostros y luego puede aplicar este conocimiento para reconocer otros objetos.

Desde una perspectiva pedagógica, a menudo aprendemos tareas primero que nos brindan las habilidades necesarias para dominar técnicas más complejas. Esto es cierto tanto para aprender la forma correcta de caer en las artes marciales, por ejemplo, Judo, como para aprender a programar.

Tomando un ejemplo de la cultura pop, también podemos considerar The Karate Kid (1984) (gracias a Margaret Mitchell y Adrian Benton por la inspiración). En la película, el sensei Sr. Miyagi le enseña al niño del karate tareas aparentemente no relacionadas, como lijar el piso y encerar un automóvil. En retrospectiva, estos, sin embargo, resultan equiparlo con habilidades invaluables que son relevantes para aprender kárate .

Finalmente, podemos motivar el aprendizaje multitarea desde el punto de vista del aprendizaje automático: podemos ver el aprendizaje multitarea como una forma de transferencia inductiva. La transferencia inductiva puede ayudar a mejorar un modelo al introducir un sesgo inductivo, lo que hace que un modelo prefiera algunas hipótesis sobre otras. Por ejemplo, una forma común de sesgo inductivo esℓ1ℓ1regularización, lo que conduce a una preferencia por soluciones dispersas. En el caso de MTL, el sesgo inductivo lo proporcionan las tareas auxiliares, lo que hace que el modelo prefiera hipótesis que expliquen más de una tarea. Como veremos en breve, esto generalmente conduce a soluciones que se generalizan mejor.

Dos métodos MTL para Deep Learning

Hasta ahora, nos hemos centrado en las motivaciones teóricas para MTL. Para hacer que las ideas de MTL sean más concretas, ahora veremos las dos formas más utilizadas para realizar el aprendizaje multitarea en redes neuronales profundas. En el contexto del aprendizaje profundo, el aprendizaje multitarea generalmente se realiza con el intercambio de parámetros duros o blandos de capas ocultas.

Compartir parámetros duros

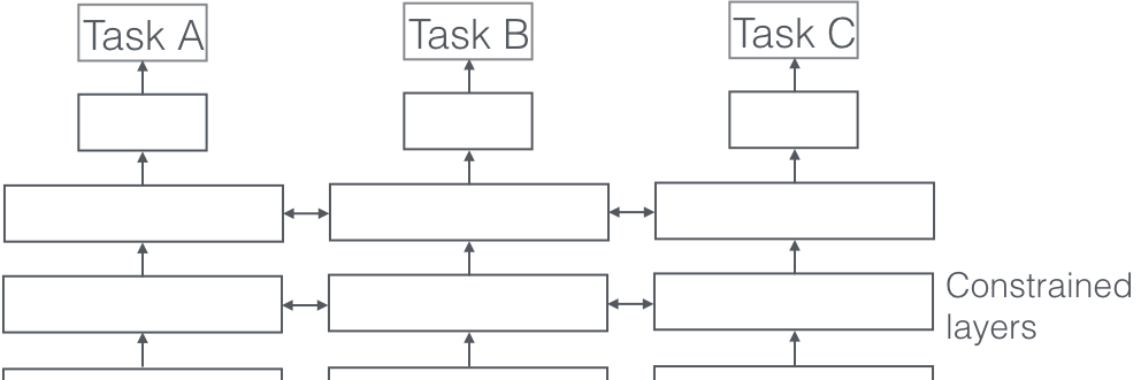
El intercambio de parámetros duros es el enfoque más utilizado para MTL en redes neuronales y se remonta a ^[6] . Generalmente se aplica compartiendo las capas ocultas entre todas las tareas, mientras se mantienen varias capas de salida específicas de la tarea.

El intercambio estricto de parámetros reduce en gran medida el riesgo de sobreajuste. De hecho, ^[7] mostró que el riesgo de sobreajustar los parámetros compartidos es un orden N, donde N es el número de tareas, menor que sobreajustar los parámetros específicos de la tarea, es decir, las capas de salida. Esto tiene sentido intuitivamente: cuantas más tareas estamos aprendiendo simultáneamente, más nuestro modelo tiene que encontrar una representación que capture todas las tareas y menor es nuestra posibilidad de sobreajustar nuestra tarea original.

Compartir parámetros suaves

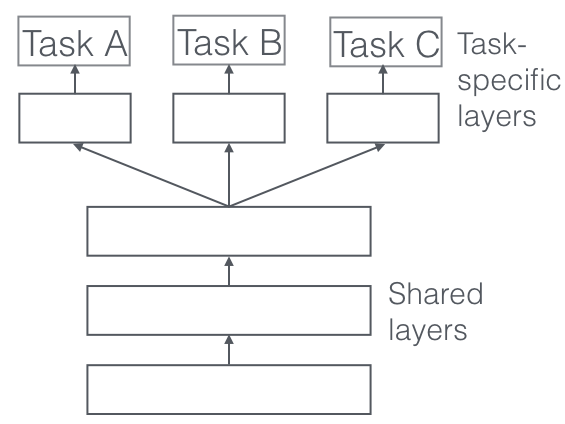
En el intercambio de parámetros suaves, por otro lado, cada tarea tiene su propio modelo con sus propios parámetros. A continuación, se regulariza la distancia entre los parámetros del modelo para fomentar que los parámetros sean similares. ^[8] por ejemplo, use elℓ2ℓ2norm para la regularización, mientras que ^[9] utiliza la norma de seguimiento.

Las restricciones utilizadas para compartir parámetros blandos en redes neuronales profundas se han inspirado en gran medida en las técnicas de regularización para MTL que se han desarrollado para otros modelos, que pronto discutiremos.

¿Por qué funciona MTL?

Aunque un sesgo inductivo obtenido a través del aprendizaje multitarea parece intuitivamente plausible, para comprender mejor MTL, debemos observar los mecanismos que subyacen a él. La mayoría de estos han sido propuestos por primera vez por Caruana (1998). Para todos los ejemplos, supondremos que tenemos dos tareas relacionadasAAyBB, que se basan en una representación de capa oculta comúnFF.

Aumento de datos implícito

MTL aumenta efectivamente el tamaño de la muestra que estamos usando para entrenar nuestro modelo. Como todas las tareas son al menos algo ruidosas, al entrenar a un modelo en alguna tareaAA, nuestro objetivo es aprender una buena representación para la tareaAAque idealmente ignora el ruido dependiente de los datos y generaliza bien. Como diferentes tareas tienen diferentes patrones de ruido, un modelo que aprende dos tareas simultáneamente puede aprender una representación más general. Aprender solo tareaAAcorre el riesgo de sobreajustarse a la tareaAA, mientras aprendeAAyBBconjuntamente permite que el modelo obtenga una mejor representaciónFFmediante el promedio de los patrones de ruido.

Centrando la atencion

Si una tarea es muy ruidosa o los datos son limitados y de gran dimensión, puede ser difícil para un modelo diferenciar entre características relevantes e irrelevantes. MTL puede ayudar al modelo a centrar su atención en las características que realmente importan, ya que otras tareas proporcionarán evidencia adicional de la relevancia o irrelevancia de esas características.

Escuchar a escondidas

Algunas caracteristicasGRAMOGRAMOson fáciles de aprender para alguna tareaBB, mientras que es difícil de aprender para otra tareaAA. Esto podría deberse a queAAinteractúa con las funciones de una manera más compleja o porque otras funciones impiden la capacidad de aprendizaje del modeloGRAMOGRAMO. A través de MTL, podemos permitir que el modelo escuche a escondidas , es decir, aprendaGRAMOGRAMOa través de la tareaBB. La forma más sencilla de hacerlo es a través de sugerencias ^[10] , es decir, entrenando directamente el modelo para predecir las características más importantes.

Sesgo de representación

MTL sesga el modelo para preferir representaciones que también prefieren otras tareas. Esto también ayudará al modelo a generalizarse a nuevas tareas en el futuro, ya que un espacio de hipótesis que funciona bien para un número suficientemente grande de tareas de entrenamiento también funcionará bien para aprender tareas novedosas siempre que sean del mismo entorno ^[11] .

Regularización

Finalmente, MTL actúa como un regularizador al introducir un sesgo inductivo. Como tal, reduce el riesgo de sobreajuste, así como la complejidad Rademacher del modelo, es decir, su capacidad para ajustar el ruido aleatorio.

MTL en modelos no neuronales

Para comprender mejor MTL en redes neuronales profundas, ahora buscaremos en la literatura existente sobre MTL modelos lineales, métodos kernel y algoritmos bayesianos. En particular, discutiremos dos ideas principales que han sido omnipresentes a lo largo de la historia del aprendizaje multitarea: hacer cumplir la escasez entre tareas a través de la regularización de normas; y modelar las relaciones entre tareas.

Tenga en cuenta que muchos enfoques de MTL en la literatura tratan con un entorno homogéneo: asumen que todas las tareas están asociadas con una sola salida, por ejemplo, el conjunto de datos MNIST multiclase generalmente se presenta como 10 tareas de clasificación binaria. Los enfoques más recientes se ocupan de un entorno más realista y heterogéneo en el que cada tarea corresponde a un conjunto único de resultados.

Regularización de bloques escasos

Para conectar mejor los siguientes enfoques, primero introduzcamos algo de notación. TenemosTTTareas. para cada tareatt, tenemos un modelometrotmetrotcon parámetrosatatde dimensionalidaddd. Podemos escribir los parámetros como un vector columnaat=[a1,t … ad,t]⊤at=[a1,t … ad,t]⊤. Ahora apilamos estos vectores de columnaa1,…,aTa1,…,aTcolumna por columna para formar una matrizA∈Rd×TA∈Rd×T. losii-ésima fila deAAentonces contiene el parámetroai,⋅ai,⋅correspondiente a laii-ésima característica del modelo para cada tarea, mientras que eljj-ésima columna deAAcontiene los parámetrosa⋅,ja⋅,jcorrespondiente a lajj-ésimo modelo.

Muchos métodos existentes hacen algunas suposiciones de escasez con respecto a los parámetros de nuestros modelos. ^[12] asume que todos los modelos comparten un pequeño conjunto de características. En términos de nuestra matriz de parámetros de tareasAA, esto significa que todas menos unas pocas filas son00, lo que corresponde a solo unas pocas funciones que se utilizan en todas las tareas. Para hacer cumplir esto, generalizan laℓ1ℓ1norma a la configuración de MTL. Recuerda que elℓ1ℓ1norma es una restricción en la suma de los parámetros, lo que obliga a que todos menos unos pocos parámetros sean exactamente00. . . . También se le conoce como lazo (__l__east __a__absolute __s__hrinkage y __s__election __o__perator).

Mientras que en la configuración de una sola tarea, elℓ1ℓ1la norma se calcula en función del vector de parámetrosatatde la tarea respectivatt, para MTL lo calculamos sobre nuestra matriz de parámetros de tareasAA. Para hacer esto, primero calculamos unℓqℓqnorma en cada filaaiaique contiene el parámetro correspondiente a laii-ésima característica en todas las tareas, lo que produce un vectorb=[|a1|q…|ad|q]∈Rdb=[|a1|q…|ad|q]∈Rd. Luego calculamos elℓ1ℓ1norma de este vector, que obliga a todas menos a unas pocas entradas debb, es decir filas enAAser – estar00.

Como podemos ver, dependiendo de la restricción que nos gustaría colocar en cada fila, podemos usar una diferenteℓqℓq. En general, nos referimos a estas restricciones de norma mixta comoℓ1/ℓqℓ1/ℓqnormas También se conocen como regularización de bloques dispersos, ya que conducen a filas enteras deAAsiendo configurado para00. ^[13] usoℓ1/ℓ∞ℓ1/ℓ∞regularización, mientras que Argyriou et al. (2007) utilizan una mezclaℓ1/ℓ2ℓ1/ℓ2norma. Este último también se conoce como grupo lazo y fue propuesto por primera vez por ^[14] .

Argyriou et al. (2007) también muestran que el problema de optimizar el lazo de grupo no convexo puede volverse convexo penalizando la norma de traza deAA, que obligaAAser de rango bajo y, por lo tanto, restringe los vectores de parámetros de columnaa⋅,1,…,a⋅,ta⋅,1,…,a⋅,tvivir en un subespacio de baja dimensión. ^[15] además, establece límites superiores para el uso del lazo grupal en el aprendizaje de tareas múltiples.

Si bien esta regularización de bloques escasos es intuitivamente plausible, depende en gran medida de la medida en que las funciones se comparten entre tareas. ^[16] muestran que si las características no se superponen mucho,ℓ1/ℓqℓ1/ℓqla regularización en realidad podría ser peor que la de los elementosℓ1ℓ1regularización

Por esta razón, ^[17] mejora los modelos de bloques dispersos al proponer un método que combina la regularización de bloques dispersos y de elementos dispersos. Descomponen la matriz de parámetros de la tarea.AAen dos matricesBBySSdóndeA=B+SA=B+S. BBluego se hace cumplir para que sea escaso en bloques usandoℓ1/ℓ∞ℓ1/ℓ∞regularización, mientrasSSse hace disperso en cuanto a los elementos usando lasso. Recientemente, ^[18] proponen una versión distribuida de regularización de grupos dispersos.

Relaciones de tareas de aprendizaje

Si bien la restricción de escasez de grupos obliga a nuestro modelo a considerar solo unas pocas funciones, estas funciones se utilizan en gran medida en todas las tareas. Por lo tanto, todos los enfoques anteriores asumen que las tareas utilizadas en el aprendizaje multitarea están estrechamente relacionadas. Sin embargo, es posible que cada tarea no esté estrechamente relacionada con todas las tareas disponibles. En esos casos, compartir información con una tarea no relacionada podría perjudicar el rendimiento, un fenómeno conocido como transferencia negativa.

En lugar de la escasez, nos gustaría aprovechar el conocimiento previo que indica que algunas tareas están relacionadas mientras que otras no. En este escenario, una restricción que imponga una agrupación de tareas podría ser más apropiada. ^[19] sugiere imponer una restricción de agrupamiento penalizando ambas normas de nuestros vectores de columnas de tareasa⋅,1,…,a⋅,ta⋅,1,…,a⋅,tasí como su varianza con la siguiente restricción:

Vaya=|¯a|2+yoT∑Tt=1|a⋅,t−¯a|2Vaya=|a¯|2+yoT∑t=1T|a⋅,t−a¯|2

dónde¯a=(∑Tt=1a⋅,t)/Ta¯=(∑t=1Ta⋅,t)/Tes el vector de parámetros medios. Esta penalización impone una agrupación de los vectores de parámetros de tareasa⋅,1,…,a⋅,ta⋅,1,…,a⋅,thacia su medio que es controlado poryoyo. Aplican esta restricción a los métodos kernel, pero es igualmente aplicable a los modelos lineales.

^[20] también propuso una restricción similar para las SVM . Su restricción está inspirada en los métodos bayesianos y busca hacer que todos los modelos se acerquen a algún modelo medio. En las SVM, la pérdida compensa tener un gran margen para cada SVM con estar cerca del modelo medio.

^[21] hacen más explícitos los supuestos que subyacen a la regularización del conglomerado al formalizar una restricción del conglomerado enAAbajo el supuesto de que el número de conglomeradosCCse sabe de antemano. Luego descomponen la pena en tres normas separadas:

• Una penalización global que mide qué tan grandes son en promedio nuestros vectores de parámetros de columna:Vayametroyanorte(A)=|¯a|2Vayametroyanorte(A)=|a¯|2.
• Una medida de la varianza entre conglomerados que mide qué tan cerca están los conglomerados entre sí: Vayabytenyynorte(A)=∑CC=1TC|¯aC−¯a|2Vayabytenyynorte(A)=∑C=1CTC|a¯C−a¯|2dóndeTCTCes el número de tareas en elCC-ésimo grupo y¯aCa¯Ces el vector medio de los vectores de parámetros de tarea en elCC-ésimo grupo.
• Una medida de la varianza dentro del grupo que mide qué tan compacto es cada grupo:Vayaenithinorte=∑CC=1∑t∈j(C)|a⋅,t−¯aC|2Vayaenithinorte=∑C=1C∑t∈j(C)|a⋅,t−a¯C|2dóndej(C)j(C)es el conjunto de tareas en elCC-ésimo grupo.

La restricción final entonces es la suma ponderada de las tres normas:

Vaya(A)=yo1Vayametroyanorte(A)+yo2Vayabytenyynorte(A)+yo3Vayaenithinorte(A)Vaya(A)=yo1Vayametroyanorte(A)+yo2Vayabytenyynorte(A)+yo3Vayaenithinorte(A).

Como esta restricción supone que los grupos se conocen de antemano, introducen una relajación convexa de la penalización anterior que permite aprender los grupos al mismo tiempo.

En otro escenario, es posible que las tareas no ocurran en clústeres pero tengan una estructura inherente. ^[22] extiende el lazo de grupo para tratar con tareas que ocurren en una estructura de árbol, mientras que ^[23] lo aplica a tareas con estructuras gráficas.

Mientras que los enfoques anteriores para modelar la relación entre tareas emplean la regularización de normas, otros enfoques lo hacen sin regularización: ^[24] fueron los primeros en presentar un algoritmo de agrupación de tareas utilizando k-vecino más cercano, mientras que ^[25] aprenden una estructura común de múltiples tareas relacionadas con una aplicación al aprendizaje semi-supervisado.

Muchos otros trabajos sobre las relaciones de tareas de aprendizaje para el aprendizaje multitarea utilizan métodos bayesianos:
^[26] proponen una red neuronal bayesiana para el aprendizaje multitarea colocando una prioridad en los parámetros del modelo para fomentar parámetros similares en todas las tareas. ^[27] extiende los procesos gaussianos (GP) a MTL infiriendo parámetros para una matriz de covarianza compartida. Como esto es computacionalmente muy costoso, adoptan un esquema de aproximación escasa que selecciona con avidez los ejemplos más informativos. ^[28] también usan GP para MTL asumiendo que todos los modelos se muestrean a partir de un previo común.

^[29] coloque una Gaussiana como una distribución previa en cada capa específica de la tarea. Para fomentar la similitud entre diferentes tareas, proponen hacer que la tarea media sea dependiente e introducir una agrupación de tareas utilizando una distribución mixta. Es importante destacar que requieren que las características de la tarea que definen los grupos y el número de mezclas se especifiquen de antemano.

Basándose en esto, ^[30] dibuje la distribución a partir de un proceso de Dirichlet y permita que el modelo aprenda la similitud entre las tareas, así como la cantidad de grupos. Luego comparten el mismo modelo entre todas las tareas en el mismo clúster. ^[31] propone un modelo bayesiano jerárquico, que aprende una jerarquía de tareas latentes, mientras que ^[32] utiliza una regularización basada en GP para MTL y amplía un enfoque anterior basado en GP para que sea computacionalmente más factible en entornos más grandes.

Otros enfoques se centran en el entorno de aprendizaje multitarea en línea: ^[33] adaptan algunos métodos existentes, como el enfoque de Evgeniou et al. (2005) a la configuración en línea. También proponen una extensión MTL del Perceptron regularizado, que codifica la relación de tareas en una matriz. Usan diferentes formas de regularización para sesgar esta matriz de relación de tareas, por ejemplo, la cercanía de los vectores característicos de la tarea o la dimensión del subespacio abarcado. Es importante destacar que, al igual que algunos enfoques anteriores, requieren que las características de la tarea que componen esta matriz se proporcionen por adelantado. ^[34] luego extienda el enfoque anterior aprendiendo la matriz de relación de tareas.

^[35] supone que las tareas forman grupos disjuntos y que las tareas dentro de cada grupo se encuentran en un subespacio de baja dimensión. Dentro de cada grupo, las tareas comparten la misma representación de características cuyos parámetros se aprenden junto con la matriz de asignación del grupo utilizando un esquema de minimización alterna. Sin embargo, una separación total entre grupos podría no ser la forma ideal, ya que las tareas aún pueden compartir algunas características que son útiles para la predicción.

^[36] a su vez permite que dos tareas de diferentes grupos se superpongan asumiendo que existe un pequeño número de tareas de base latente. Luego modelan el vector de parámetrosatatde cada tarea realttcomo una combinación lineal de estos:at=Lstat=LstdóndeL ∈Rk×dL ∈Rk×des una matriz que contiene los vectores de parámetros dekktareas latentes, mientrasst ∈Rkst ∈Rkes un vector que contiene los coeficientes de la combinación lineal. Además, obligan a que la combinación lineal sea escasa en las tareas latentes; la superposición en los patrones de escasez entre dos tareas controla la cantidad de intercambio entre estas. Finalmente, ^[37] aprende un pequeño grupo de hipótesis compartidas y luego asigna cada tarea a una sola hipótesis.

Trabajo reciente sobre MTL para aprendizaje profundo

Si bien muchos enfoques recientes de aprendizaje profundo han utilizado el aprendizaje de tareas múltiples, ya sea explícita o implícitamente, como parte de su modelo (los ejemplos destacados se presentarán en la siguiente sección), todos emplean los dos enfoques que presentamos anteriormente, duro y blando. intercambio de parámetros. Por el contrario, solo unos pocos artículos han analizado el desarrollo de mejores mecanismos para MTL en redes neuronales profundas.

Redes de relaciones profundas

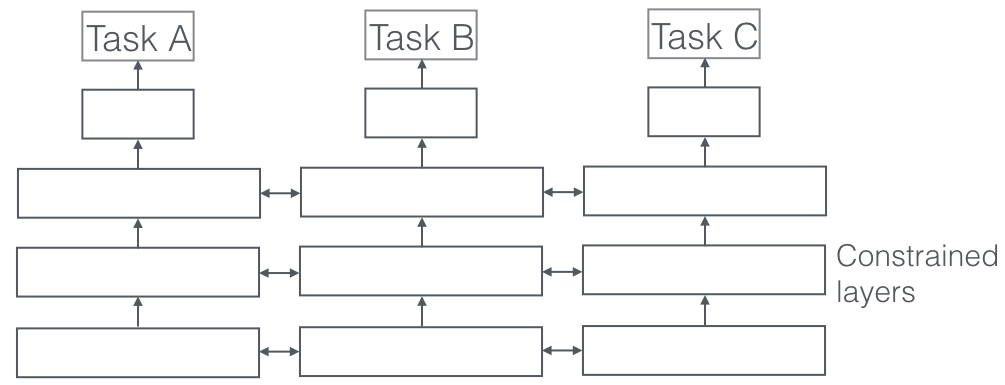
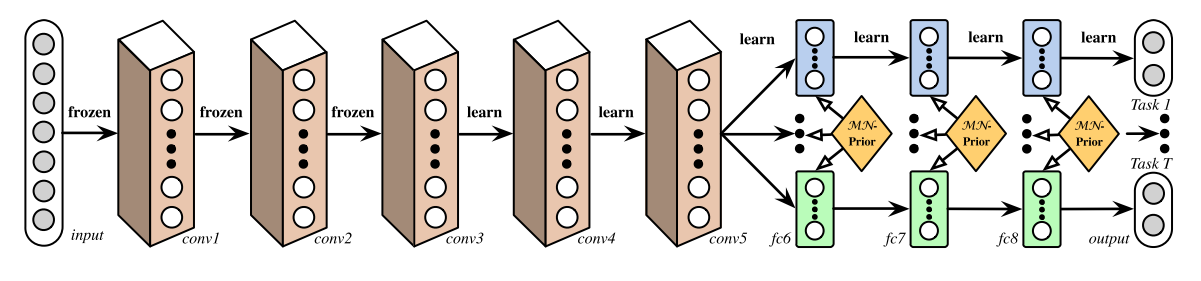
En MTL para visión por computadora, los enfoques a menudo comparten las capas convolucionales, mientras aprenden capas totalmente conectadas específicas de la tarea. ^[38] mejoran estos modelos proponiendo Redes de Relaciones Profundas. Además de la estructura de capas compartidas y específicas de tareas, que se puede ver en la Figura 3, colocan matrices previas en las capas completamente conectadas, lo que permite que el modelo aprenda la relación entre tareas, similar a algunos de los modelos bayesianos que usamos. haber mirado antes. Este enfoque, sin embargo, todavía se basa en una estructura predefinida para compartir, que puede ser adecuada para problemas de visión por computadora bien estudiados, pero puede resultar propenso a errores para tareas novedosas.

Uso compartido de funciones totalmente adaptable

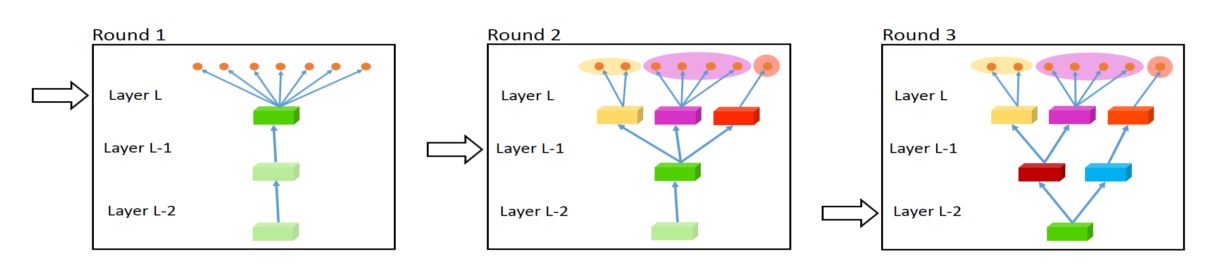
Comenzando en el otro extremo, ^[39] propone un enfoque de abajo hacia arriba que comienza con una red delgada y la amplía dinámicamente con avidez durante el entrenamiento utilizando un criterio que promueve la agrupación de tareas similares. El procedimiento de ampliación, que crea ramas de forma dinámica, se puede ver en la Figura 4. Sin embargo, es posible que el método voraz no pueda descubrir un modelo que sea globalmente óptimo, mientras que asignar cada rama exactamente a una tarea no permite que el modelo aprenda cosas más complejas. interacciones entre tareas.

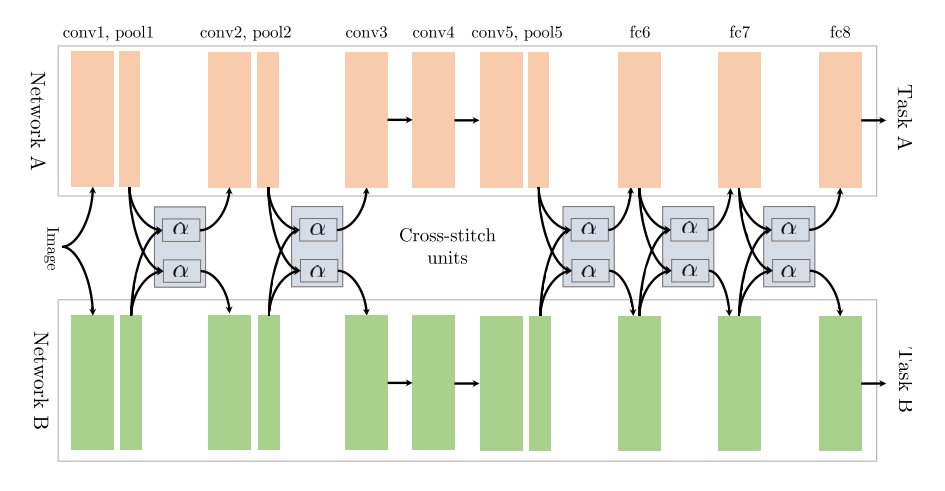
Punto de Cruz Redes

^[40] comienzan con dos arquitecturas de modelo separadas al igual que en el intercambio de parámetros suaves. Luego usan lo que llaman unidades de punto de cruz para permitir que el modelo determine de qué manera las redes específicas de la tarea aprovechan el conocimiento de la otra tarea al aprender una combinación lineal de la salida de las capas anteriores. Su arquitectura se puede ver en la Figura 5, en la que solo colocan unidades de punto de cruz después de agrupar y unir completamente las capas.

Baja supervisión

Por el contrario, en el procesamiento del lenguaje natural (NLP), el trabajo reciente se centró en encontrar mejores jerarquías de tareas para el aprendizaje de tareas múltiples: ^[41] muestran que las tareas de bajo nivel, es decir, las tareas de NLP que se usan típicamente para el preprocesamiento, como el etiquetado de parte del discurso y el reconocimiento de entidades nombradas, debe ser supervisado en las capas inferiores cuando se utiliza como tarea auxiliar.

Un modelo conjunto de muchas tareas

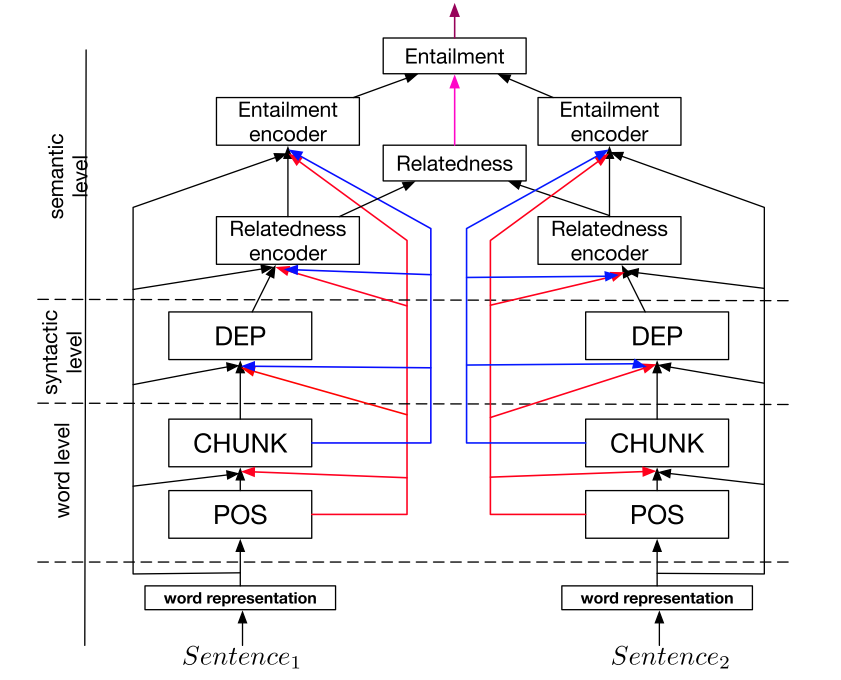
Sobre la base de este hallazgo, ^[42] predefine una arquitectura jerárquica que consta de varias tareas de PNL, que se puede ver en la Figura 6, como un modelo conjunto para el aprendizaje de tareas múltiples.

Ponderación de pérdidas con incertidumbre

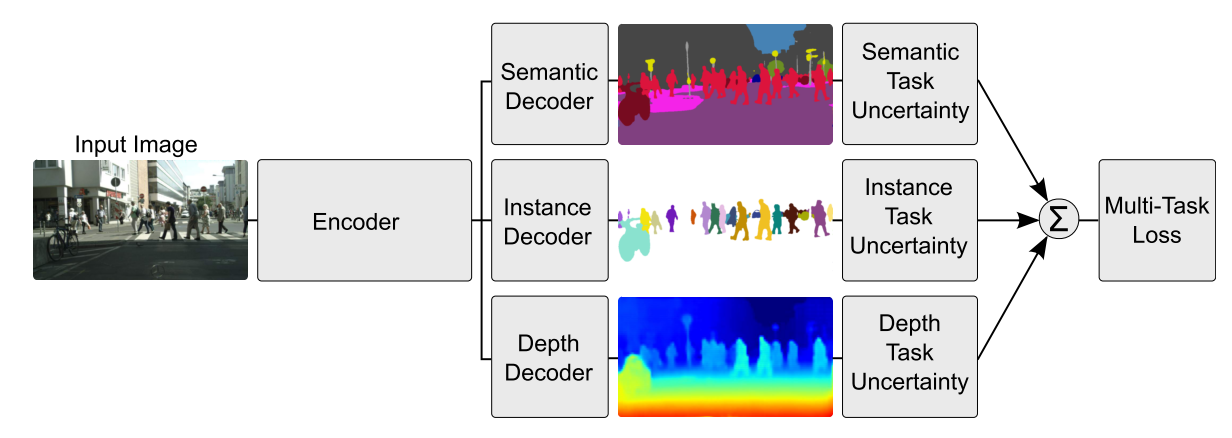
En lugar de aprender la estructura de compartir, ^[43] adopte un enfoque ortogonal considerando la incertidumbre de cada tarea. Luego ajustan el peso relativo de cada tarea en la función de costo al derivar una función de pérdida de tareas múltiples basada en maximizar la probabilidad gaussiana con incertidumbre dependiente de la tarea. Su arquitectura para la regresión de profundidad por píxel, la segmentación semántica y de instancias se puede ver en la Figura 7.

Tensorización factorial para MTL

El trabajo más reciente busca generalizar los enfoques existentes de MTL para el aprendizaje profundo: ^[44] generalizar algunos de los enfoques de factorización de matriz discutidos anteriormente utilizando la factorización de tensor para dividir los parámetros del modelo en parámetros compartidos y específicos de la tarea para cada capa.

Redes de Esclusas

Finalmente, proponemos Sluice Networks ^[45] , un modelo que generaliza los enfoques MTL basados ​​en Deep Learning, como compartir parámetros duros y redes de punto de cruz, enfoques de regularización de bloques dispersos, así como enfoques recientes de NLP que crean una jerarquía de tareas. El modelo, que se puede ver en la Figura 8, permite conocer qué capas y subespacios se deben compartir, así como en qué capas la red ha aprendido las mejores representaciones de las secuencias de entrada.

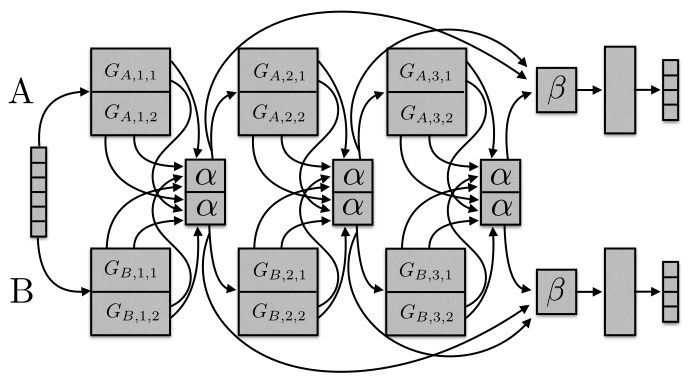
¿Qué debo compartir en mi modelo?

Habiendo examinado estos enfoques recientes, resumamos brevemente y saquemos una conclusión sobre qué compartir en nuestros modelos MTL profundos. La mayoría de los enfoques en la historia de MTL se han centrado en el escenario donde las tareas se extraen de la misma distribución (Baxter, 1997). Si bien este escenario es beneficioso para compartir, no siempre se cumple. Para desarrollar modelos robustos para MTL, tenemos que ser capaces de lidiar con tareas no relacionadas o solo vagamente relacionadas.

Si bien el trabajo inicial en MTL para Deep Learning ha especificado previamente qué capas compartir para cada emparejamiento de tareas, esta estrategia no escala y sesga en gran medida las arquitecturas MTL. El intercambio de parámetros duros, una técnica propuesta originalmente por Caruana (1996), sigue siendo la norma 20 años después. Si bien es útil en muchos escenarios, el uso compartido de parámetros duros se descompone rápidamente si las tareas no están estrechamente relacionadas o requieren razonamiento en diferentes niveles. Por lo tanto, los enfoques recientes han buscado aprender qué compartir y, en general, superan el intercambio de parámetros duros. Además, es útil dar a nuestros modelos la capacidad de aprender una jerarquía de tareas, particularmente en casos que requieren diferentes granularidades.

Como se mencionó inicialmente, estamos haciendo MTL tan pronto como estamos optimizando más de una función de pérdida. En lugar de restringir nuestro modelo para comprimir el conocimiento de todas las tareas en el mismo espacio de parámetros, es útil aprovechar los avances en MTL que hemos discutido y permitir que nuestro modelo aprenda cómo las tareas deben interactuar entre sí.

Tareas auxiliares

MTL encaja naturalmente en situaciones en las que estamos interesados ​​en obtener predicciones para múltiples tareas a la vez. Tales escenarios son comunes, por ejemplo, en pronósticos financieros o económicos, en los que podríamos querer predecir el valor de muchos indicadores posiblemente relacionados, o en bioinformática, donde podríamos querer predecir síntomas de múltiples enfermedades simultáneamente. En escenarios como el descubrimiento de fármacos, donde se deben predecir decenas o cientos de compuestos activos, la precisión de MTL aumenta continuamente con la cantidad de tareas (Ramsundar et al., 2015).

En la mayoría de las situaciones, sin embargo, solo nos preocupamos por el desempeño en una tarea. En esta sección, veremos cómo podemos encontrar una tarea auxiliar adecuada para seguir cosechando los beneficios del aprendizaje multitarea.

Tarea relacionada

Usar una tarea relacionada como tarea auxiliar para MTL es la elección clásica. Para tener una idea de lo que puede ser una tarea relacionada, presentaremos algunos ejemplos destacados. Caruana (1998) utiliza tareas que predicen diferentes características de la carretera como tareas auxiliares para predecir la dirección de la dirección en un automóvil autónomo; ^[46] utilizan la estimación de la postura de la cabeza y la inferencia de atributos faciales como tareas auxiliares para la detección de puntos de referencia faciales; ^[47] aprender conjuntamente clasificación de consultas y búsqueda web; Girshick (2015) predice conjuntamente la clase y las coordenadas de un objeto en una imagen; finalmente, ^[48] predicen conjuntamente la duración de los fonemas y el perfil de frecuencia para la conversión de texto a voz.

Adversario

A menudo, los datos etiquetados para una tarea relacionada no están disponibles. En algunas circunstancias, sin embargo, tenemos acceso a una tarea que es opuesta a lo que queremos lograr. Estos datos se pueden aprovechar utilizando una pérdida de adversario, que no busca minimizar sino maximizar el error de entrenamiento utilizando una capa de inversión de gradiente. Esta configuración ha encontrado un éxito reciente en la adaptación del dominio ^[49] . La tarea contradictoria en este caso es predecir el dominio de la entrada; al invertir el gradiente de la tarea contradictoria, se maximiza la pérdida de la tarea contradictoria, lo que es beneficioso para la tarea principal, ya que obliga al modelo a aprender representaciones que no pueden distinguir entre dominios.

Sugerencias

Como se mencionó anteriormente, MTL se puede usar para aprender características que pueden no ser fáciles de aprender simplemente usando la tarea original. Una forma efectiva de lograr esto es usar sugerencias, es decir, predecir las características como una tarea auxiliar. Ejemplos recientes de esta estrategia en el contexto del procesamiento del lenguaje natural son ^[50] quienes predicen si una oración de entrada contiene una palabra de sentimiento positivo o negativo como tareas auxiliares para el análisis de sentimiento y ^[51] quienes predicen si un nombre está presente en una oración como tarea auxiliar para la detección de errores de nombre.

Centrando la atención

De manera similar, la tarea auxiliar se puede utilizar para centrar la atención en partes de la imagen que una red normalmente ignoraría. Por ejemplo, para aprender a conducir (Caruana, 1998), un modelo de una sola tarea normalmente podría ignorar las marcas de los carriles, ya que constituyen solo una pequeña parte de la imagen y no siempre están presentes. Sin embargo, la predicción de marcas de carril como tarea auxiliar obliga al modelo a aprender a representarlas; este conocimiento también se puede utilizar para la tarea principal. De manera análoga, para el reconocimiento facial, uno podría aprender a predecir la ubicación de los puntos de referencia faciales como tareas auxiliares, ya que estos suelen ser distintivos.

Suavizado de cuantización

Para muchas tareas, el objetivo de entrenamiento está cuantificado, es decir, mientras que una escala continua podría ser más plausible, las etiquetas están disponibles como un conjunto discreto. Este es el caso en muchos escenarios que requieren evaluación humana para la recopilación de datos, como predecir el riesgo de una enfermedad (por ejemplo, bajo/medio/alto) o análisis de sentimiento (positivo/neutral/negativo). El uso de tareas auxiliares menos cuantificadas podría ayudar en estos casos, ya que podrían aprenderse más fácilmente debido a que su objetivo es más fluido.

Entradas de predicción

En algunos escenarios, no es práctico usar algunas funciones como entradas, ya que no son útiles para predecir el objetivo deseado. Sin embargo, es posible que aún puedan guiar el aprendizaje de la tarea. En esos casos, las funciones se pueden utilizar como salidas en lugar de entradas. ^[52] presentan varios problemas donde esto es aplicable.

Usar el futuro para predecir el presente

En muchas situaciones, algunas funciones solo están disponibles después de que se supone que se deben realizar las predicciones. Por ejemplo, para los automóviles autónomos, se pueden realizar mediciones más precisas de los obstáculos y las marcas de carril una vez que el automóvil los rebasa. Caruana (1998) también da el ejemplo de la predicción de neumonía, después de lo cual estarán disponibles los resultados de ensayos médicos adicionales. Para estos ejemplos, los datos adicionales no se pueden usar como funciones, ya que no estarán disponibles como entrada en tiempo de ejecución. Sin embargo, puede usarse como una tarea auxiliar para impartir conocimientos adicionales al modelo durante el entrenamiento.

Aprendizaje de representación

El objetivo de una tarea auxiliar en MTL es permitir que el modelo aprenda representaciones que son compartidas o útiles para la tarea principal. Todas las tareas auxiliares discutidas hasta ahora hacen esto implícitamente: están estrechamente relacionadas con la tarea principal, por lo que aprenderlas probablemente le permita al modelo aprender representaciones beneficiosas. Es posible un modelado más explícito, por ejemplo, empleando una tarea que se sabe que permite que un modelo aprenda representaciones transferibles. El objetivo de modelado del lenguaje empleado por Cheng et al. (2015) y ^[53] cumple este papel. De manera similar, un objetivo de codificador automático también se puede utilizar como tarea auxiliar.

¿Qué tareas auxiliares son útiles?

En esta sección, hemos discutido diferentes tareas auxiliares que se pueden usar para aprovechar MTL, incluso si solo nos preocupamos por una tarea. Sin embargo, todavía no sabemos qué tarea auxiliar será útil en la práctica. Encontrar una tarea auxiliar se basa en gran medida en la suposición de que la tarea auxiliar debería estar relacionada con la tarea principal de alguna manera y que debería ser útil para predecir la tarea principal.

Sin embargo, todavía no tenemos una buena noción de cuándo dos tareas deben considerarse similares o relacionadas. Caruana (1998) define dos tareas como similares si utilizan las mismas características para tomar una decisión. Baxter (2000) argumenta sólo teóricamente que las tareas relacionadas comparten una clase de hipótesis óptima común, es decir, tienen el mismo sesgo inductivo. ^[54] proponen que dos tareas sonFF-relacionado si los datos para ambas tareas se pueden generar a partir de una distribución de probabilidad fija utilizando un conjunto de transformacionesFF. Si bien esto permite razonar sobre tareas en las que diferentes sensores recopilan datos para el mismo problema de clasificación, por ejemplo, reconocimiento de objetos con datos de cámaras con diferentes ángulos y condiciones de iluminación, no es aplicable a tareas que no abordan el mismo problema. Xue et al. (2007) finalmente argumentan que dos tareas son similares si sus límites de clasificación, es decir, los vectores de parámetros están cerca.

A pesar de estos primeros avances teóricos en la comprensión de la relación entre tareas, no hemos hecho mucho progreso reciente hacia este objetivo. La similitud de tareas no es binaria, sino que reside en un espectro. Más tareas similares deberían ayudar más en MTL, mientras que tareas menos similares deberían ayudar menos. Permitir que nuestros modelos aprendan qué compartir con cada tarea podría permitirnos eludir temporalmente la falta de teoría y hacer un mejor uso incluso de las tareas relacionadas de forma vaga. Sin embargo, también necesitamos desarrollar una noción más basada en principios de similitud de tareas con respecto al aprendizaje de tareas múltiples para saber qué tareas deberíamos preferir.

Trabajos recientes ^[55] han encontrado que las tareas auxiliares con distribuciones de etiquetas compactas y uniformes son preferibles para los problemas de etiquetado de secuencias en NLP, lo que hemos confirmado en experimentos (Ruder et al., 2017). Además, se ha encontrado que las ganancias son más probables para las tareas principales que se estancan rápidamente con las tareas auxiliares que no se estancan ^[56] .

Estos experimentos, sin embargo, hasta ahora han tenido un alcance limitado y los hallazgos recientes solo brindan las primeras pistas para una comprensión más profunda del aprendizaje multitarea en redes neuronales.

Conclusión

En esta descripción general, he revisado tanto la historia de la literatura sobre el aprendizaje multitarea como el trabajo más reciente sobre MTL para el aprendizaje profundo. Si bien MTL se usa con más frecuencia, el paradigma de uso compartido de parámetros duros de 20 años sigue siendo generalizado para MTL basado en redes neuronales. Sin embargo, los avances recientes sobre cómo aprender qué compartir son prometedores. Al mismo tiempo, nuestra comprensión de las tareas (su similitud, relación, jerarquía y beneficio para MTL) aún es limitada y necesitamos aprender más sobre ellas para obtener una mejor comprensión de las capacidades de generalización de MTL con respecto a profundidad. Redes neuronales.

Espero que haya encontrado útil esta descripción general. Si cometí algún error, me perdí una referencia o tergiversé algún aspecto, o si simplemente desea compartir sus pensamientos, deje un comentario a continuación.

Versión imprimible y cita

Esta publicación de blog también está disponible como artículo en arXiv , en caso de que quiera consultarla más adelante.

En caso de que lo haya encontrado útil, considere citar el artículo de arXiv correspondiente como:
Sebastian Ruder (2017). Una descripción general del aprendizaje multitarea en redes neuronales profundas. preimpresión de arXiv arXiv:1706.05098.

1. Collobert, R. y Weston, J. (2008). Una arquitectura unificada para el procesamiento del lenguaje natural. Actas de la 25.ª Conferencia internacional sobre aprendizaje automático – ICML ’08, 20(1), 160–167. https://doi.org/10.1145/1390156.1390177 ↩︎
2. Deng, L., Hinton, GE y Kingsbury, B. (2013). Nuevos tipos de aprendizaje de redes neuronales profundas para el reconocimiento de voz y aplicaciones relacionadas: una descripción general. Conferencia internacional IEEE de 2013 sobre procesamiento de señales, voz y acústica, 8599–8603. https://doi.org/10.1109/ICASSP.2013.6639344 ↩︎
3. Girshick, R. (2015). R-CNN rápido. En Actas de la Conferencia Internacional IEEE sobre Visión por Computador (págs. 1440–1448). https://doi.org/10.1109/iccv.2015.169 ↩︎
4. Ramsundar, B., Kearnes, S., Riley, P., Webster, D., Konerding, D. y Pande, V. (2015). Redes masivamente multitarea para el descubrimiento de fármacos. https://doi.org/https://arxiv.org/abs/1502.02072 ↩︎
5. Caruana, R. (1998). Aprendizaje multitarea. Agentes autónomos y sistemas multiagente, 27(1), 95–133. https://doi.org/10.1016/j.csl.2009.08.003 ↩︎
6. Caruana, R. “Aprendizaje multitarea: una fuente de sesgo inductivo basada en el conocimiento”. Actas de la Décima Conferencia Internacional sobre Aprendizaje Automático. 1993. ↩︎
7. Baxter, J. (1997). Un modelo bayesiano/teórico de la información de aprender a aprender a través del muestreo de tareas múltiples. Aprendizaje automático, 28, 7–39. Obtenido de http://link.springer.com/article/10.1023/A:1007327622663 ↩︎
8. Duong, L., Cohn, T., Bird, S. y Cook, P. (2015). Análisis de baja dependencia de recursos: uso compartido de parámetros entre idiomas en un analizador de red neuronal. Actas de la 53.ª Reunión Anual de la Asociación de Lingüística Computacional y la 7.ª Conferencia Internacional Conjunta sobre Procesamiento del Lenguaje Natural (Artículos Cortos), 845–850. ↩︎
9. Yang, Y., & Hospedales, TM (2017). Trace Norm Aprendizaje multitarea profundo regularizado. En la pista del taller – ICLR 2017. Obtenido de http://arxiv.org/abs/1606.04038 ↩︎
10. Abu-Mostafa, YS (1990). Aprendiendo de sugerencias en redes neuronales. Revista de Complejidad, 6(2), 192–198. https://doi.org/10.1016/0885-064X(90)90006-Y ↩︎
11. Baxter, J. (2000). Un modelo de aprendizaje de sesgo inductivo. Revista de Investigación de Inteligencia Artificial, 12, 149–198. ↩︎
12. Argyriou, A. y Pontil, M. (2007). Aprendizaje de funciones multitarea. En Avances en Sistemas de Procesamiento de Información Neural. http://doi.org/10.1007/s10994-007-5040-8 ↩︎
13. C.Zhang y J.Huang. Modelo de consistencia de selección de la selección de lazo en regresión lineal de alta dimensión. Anales de Estadística, 36:1567–1594, 2008 ↩︎
14. Yuan, Ming y Yi Lin. “Selección y estimación de modelos en regresión con variables agrupadas”. Journal of the Royal Statistical Society: Serie B (Metodología estadística) 68.1 (2006): 49-67. ↩︎
15. Lounici, K., Pontil, M., Tsybakov, AB y van de Geer, S. (2009). Aprovechando la escasez en el aprendizaje multitarea. Estado, (1). Obtenido de http://arxiv.org/pdf/0903.1468 ↩︎
16. Negahban, S. y Wainwright, MJ (2008). Recuperación de soporte conjunto bajo escalado de alta dimensión: Beneficios y peligros deℓ1,∞ℓ1,∞-regularización. Avances en los sistemas de procesamiento de información neuronal, 1161–1168. ↩︎
17. Jalali, A., Ravikumar, P., Sanghavi, S. y Ruan, C. (2010). Un modelo sucio para el aprendizaje multitarea. Avances en Sistemas de Procesamiento de Información Neural. Obtenido de https://papers.nips.cc/paper/4125-a-dirty-model-for-multi-task-learning.pdf ↩︎
18. Liu, S., Pan, SJ y Ho, Q. (2016). Aprendizaje relacional multitarea distribuido. En Actas de la 19.ª Conferencia Internacional sobre Inteligencia Artificial y Estadísticas (AISTATS) (págs. 751–760). Obtenido de http://arxiv.org/abs/1612.04022 ↩︎
19. Evgeniou, T., Micchelli, C. y Pontil, M. (2005). Aprendizaje de múltiples tareas con métodos kernel. Revista de investigación de aprendizaje automático, 6, 615–637. Obtenido de http://discovery.ucl.ac.uk/13423/ ↩︎
20. Evgeniou, T. y Pontil, M. (2004). Aprendizaje multitarea regularizado. Conferencia Internacional sobre Descubrimiento de Conocimiento y Minería de Datos, 109. https://doi.org/10.1145/1014052.1014067 ↩︎
21. Jacob, L., Vert, J., Bach, FR y Vert, J. (2009). Aprendizaje multitarea agrupado: una formulación convexa. Avances en sistemas de procesamiento de información neuronal 21, 745–752. Obtenido de http://eprints.pascal-network.org/archive/00004705/\nhttp://papers.nips.cc/paper/3499-clustered-multi-task-learning-a-convex-formulation.pdf ↩︎
22. Kim, S. y Xing, EP (2010). Lazo de grupo guiado por árbol para regresión multitarea con dispersión estructurada. 27.ª Conferencia internacional sobre aprendizaje automático, 1–14. https://doi.org/10.1214/12-AOAS549 ↩︎
23. Chen, X., Kim, S., Lin, Q., Carbonell, JG y Xing, EP (2010). Regresión multitarea estructurada por gráficos y un método de optimización eficiente para Lasso fusionado general, 1–21. https://doi.org/10.1146/annurev.arplant.56.032604.144204 ↩︎
24. Thrun, S. y O’Sullivan, J. (1996). Descubriendo la Estructura en Múltiples Tareas de Aprendizaje: El Algoritmo TC. Actas de la Decimotercera Conferencia Internacional sobre Aprendizaje Automático, 28(1), 5–5. Obtenido de http://scholar.google.com/scholar?cluster=956054018507723832&hl=en ↩︎
25. Ando, ​​RK y Tong, Z. (2005). Un marco para el aprendizaje de estructuras predictivas a partir de múltiples tareas y datos sin etiquetar. Revista de investigación de aprendizaje automático, 6, 1817–1853. ↩︎
26. Heskes, T. (2000). Bayesiano empírico para aprender a aprender. Actas de la Decimoséptima Conferencia Internacional sobre Aprendizaje Automático, 367–364. ↩︎
27. Lawrence, ND y Platt, JC (2004). Aprendiendo a aprender con la máquina de vectores informativos. XXI Conferencia Internacional sobre Aprendizaje Automático – ICML ’04, 65. https://doi.org/10.1145/1015330.1015382 ↩︎
28. Yu, K., Tresp, V. y Schwaighofer, A. (2005). Aprendizaje de procesos gaussianos a partir de múltiples tareas. Actas de la Conferencia Internacional sobre Aprendizaje Automático (ICML), 22, 1012–1019. https://doi.org/10.1145/1102351.1102479 ↩︎
29. Bakker, B. y Heskes, T. (2003). Agrupación de tareas y gating para el aprendizaje multitarea bayesiano. Revista de investigación de aprendizaje automático, 1(1), 83–99. https://doi.org/10.1162/153244304322765658 ↩︎
30. Xue, Y., Liao, X., Carin, L. y Krishnapuram, B. (2007). Aprendizaje multitarea para clasificación con procesos previos de Dirichlet. Revista de investigación de aprendizaje automático, 8, 35–63. ↩︎
31. Daume III, H. (2009). Aprendizaje multitarea bayesiano con jerarquías latentes, 135–142. Obtenido de http://dl.acm.org.sci-hub.io/citation.cfm?id=1795131 ↩︎
32. Zhang, Y. y Yeung, D. (2010). Una formulación convexa para las relaciones de tareas de aprendizaje en el aprendizaje de tareas múltiples. Uai, 733–442. ↩︎
33. Cavallanti, G., Cesa-Bianchi, N. y Gentile, C. (2010). Algoritmos lineales para la clasificación multitarea en línea. Revista de investigación de aprendizaje automático, 11, 2901–2934. ↩︎
34. Saha, A., Rai, P., Daumé, H. y Venkatasubramanian, S. (2011). Aprendizaje en línea de múltiples tareas y sus relaciones. Revista de investigación de aprendizaje automático, 15, 643–651. Obtenido de http://www.scopus.com/inward/record.url?eid=2-s2.0-84862275213&partnerID=tZOtx3y1 ↩︎
35. Kang, Z., Grauman, K. y Sha, F. (2011). Aprender con quién compartir en el aprendizaje de funciones multitarea. Actas de la 28.ª Conferencia Internacional sobre Aprendizaje Automático, (4), 4–5. Obtenido de http://machinelearning.wustl.edu/mlpapers/paper_files/ICML2011Kang_344.pdf ↩︎
36. Kumar, A. y Daumé III, H. (2012). Agrupación de tareas de aprendizaje y superposición en el aprendizaje multitarea. Actas de la 29.ª Conferencia internacional sobre aprendizaje automático, 1383–1390. ↩︎
37. Crammer, K. y Mansour, Y. (2012). Aprendizaje de tareas múltiples utilizando hipótesis compartidas. Sistemas de procesamiento de información neuronal (NIPS), 1484–1492 ↩︎
38. Long, M. y Wang, J. (2015). Aprendizaje de tareas múltiples con redes de relaciones profundas. arXiv Preimpresión arXiv:1506.02117. Obtenido de http://arxiv.org/abs/1506.02117 ↩︎
39. Lu, Y., Kumar, A., Zhai, S., Cheng, Y., Javidi, T. y Feris, R. (2016). Uso compartido de características totalmente adaptativo en redes multitarea con aplicaciones en la clasificación de atributos de persona. Obtenido de http://arxiv.org/abs/1611.05377 ↩︎
40. Misra, I., Shrivastava, A., Gupta, A. y Hebert, M. (2016). Redes de punto de cruz para el aprendizaje multitarea. En Actas de la Conferencia IEEE sobre visión artificial y reconocimiento de patrones. https://doi.org/10.1109/CVPR.2016.433 ↩︎
41. Søgaard, A. y Goldberg, Y. (2016). Aprendizaje profundo de múltiples tareas con tareas de bajo nivel supervisadas en capas inferiores. Actas de la 54.ª Reunión Anual de la Asociación de Lingüística Computacional, 231–235. ↩︎
42. Hashimoto, K., Xiong, C., Tsuruoka, Y. y Socher, R. (2016). Un modelo conjunto de muchas tareas: crecimiento de una red neuronal para múltiples tareas de PNL. arXiv Preimpresión arXiv:1611.01587. Obtenido de http://arxiv.org/abs/1611.01587 ↩︎
43. Kendall, A., Gal, Y. y Cipolla, R. (2017). Aprendizaje multitarea utilizando la incertidumbre para sopesar las pérdidas en la geometría y la semántica de la escena. Obtenido de http://arxiv.org/abs/1705.07115 ↩︎
44. Yang, Y., & Hospedales, T. (2017). Aprendizaje profundo de representación multitarea: un enfoque de factorización tensorial. En ICLR 2017. https://doi.org/10.1002/joe.20070 ↩︎
45. Ruder, S., Bingel, J., Augenstein, I. y Søgaard, A. (2017). Redes de esclusas: aprender qué compartir entre tareas vagamente relacionadas. Obtenido de http://arxiv.org/abs/1705.08142 ↩︎
46. Zhang, Z., Luo, P., Loy, CC y Tang, X. (2014). Detección de puntos de referencia faciales mediante aprendizaje multitarea profundo. En European Conference on Computer Vision (págs. 94–108). https://doi.org/10.1007/978-3-319-10599-4_7 ↩︎
47. Liu, X., Gao, J., He, X., Deng, L., Duh, K. y Wang, Y.-Y. (2015). Aprendizaje de representación utilizando redes neuronales profundas multitarea para clasificación semántica y recuperación de información. Naacl-2015, 912–921. ↩︎
48. Arık, S. Ö., Chrzanowski, M., Coates, A., Diamos, G., Gibiansky, A., Kang, Y., … Shoeybi, M. (2017). Voz profunda: texto a voz neuronal en tiempo real. En ICML 2017. ↩︎
49. Ganin, Y. y Lempitsky, V. (2015). Adaptación de dominio no supervisada por retropropagación. En Actas de la 32.ª Conferencia Internacional sobre Aprendizaje Automático. (Vol. 37). ↩︎
50. Yu, J. y Jiang, J. (2016). Aprendizaje de incrustaciones de oraciones con tareas auxiliares para la clasificación de sentimientos entre dominios. Actas de la Conferencia de 2016 sobre métodos empíricos en el procesamiento del lenguaje natural (EMNLP2016), 236–246. Obtenido de http://www.aclweb.org/anthology/D/D16/D16-1023.pdf ↩︎
51. Cheng, H., Fang, H. y Ostendorf, M. (2015). Detección de errores de nombre de dominio abierto mediante un RNN multitarea. En Actas de la Conferencia de 2015 sobre métodos empíricos en el procesamiento del lenguaje natural (págs. 737–746). ↩︎
52. Caruana, R. y Sa, VR de. (1997). Promoción de características deficientes a los supervisores: algunas entradas funcionan mejor como salidas. Advances in Neural Information Processing Systems 9: Proceedings of The 1996 Conference, 9, 389. Obtenido de http://scholar.google.com/scholar?start=20&q=author:”Rich+Caruana”&hl=en#6 ↩︎
53. Rey, M. (2017). Aprendizaje multitarea semisupervisado para el etiquetado de secuencias. En ACL 2017. ↩︎
54. Ben-David, S. y Schuller, R. (2003). Explotación de la relación de tareas para el aprendizaje de tareas múltiples. Teoría del aprendizaje y máquinas del núcleo, 567–580. https://doi.org/10.1007/978-3-540-45167-9_41 ↩︎
55. Alonso, HM y Plank, B. (2017). ¿Cuándo es efectivo el aprendizaje multitarea? Aprendizaje multitarea para la predicción de secuencias semánticas en diferentes condiciones de datos. En EACL. Obtenido de http://arxiv.org/abs/1612.02251 ↩︎
56. Bingel, J. y Søgaard, A. (2017). Identificar relaciones de tareas beneficiosas para el aprendizaje multitarea en redes neuronales profundas. En EACL. Obtenido de http://arxiv.org/abs/1702.08303 ↩︎